Die Kunst der Mathematik
Für die Autorin ist die Mathematik die schönste und leider missverstandenste Wissenschaft, die es gibt. Und sie geht sogar noch weiter mit der Behauptung, Mathematik sei eine Kunstform. Eine Liebeserklärung an die Königin der Wissenschaften.
Was passiert bei Ihnen, wenn Sie hier lesen, dass es um Mathematik gehen wird? Die ersten von Ihnen brechen den Artikel vielleicht hier ab, weil sich ein Unbehagen einstellt, das in der Schulzeit wurzelt:
Angst: „Das habe ich noch nie verstanden.“
Zweifel an der Sinnhaftigkeit: „Das brauche ich später nie wieder.“
Frustration: „Mathematik kann man oder eben nicht.“
Es gibt sogar einen verbreiteten Alptraum, der sich hartnäckig bis ins hohe Alter festsetzt, in dem man morgens vor der Matheabschlussprüfung aufwacht, aber nicht gelernt hat.
So ist es kaum verwunderlich, dass Mathematik im Leben der meisten Menschen keine bewusste Rolle mehr spielt.
Dann gibt es aber noch diejenigen, denen Mathematik als Werkzeug dient. Die Ingenieur-, Natur- und einige Sozialwissenschaften bezeichnen sie als Sprache, in der Phänomene ausgedrückt und bearbeitet werden können.
Sollten Sie noch bei mir sein: Bitte schenken Sie mir noch ein bisschen Aufmerksamkeit auf einer kleinen Reise. Vor allem, falls Sie Kinder im Schulalter haben, denn neben Verdrossenheit und Pragmatismus gibt es eine weitere Perspektive auf die Mathematik, die meiner Meinung nach die Voraussetzung ist, um eine gute Mathematiklehrerin bzw. ein guter Mathematiklehrer zu sein: Ästhetik. Wie es gelingen kann, sich die Schönheit der Mathematik zu erschließen, sodass sie zur Kunstform gerät.
Bevor wir uns also auf die Behauptung stürzen, die strenge, regelverliebte Mathematik könne mit genüsslicher Kontemplation oder gar Fantasie in Einklang gebracht werden, möchte ich kurz erklären, warum es sinnvoll sein kann, sich scheinbar zweckfrei mit ihr auseinanderzusetzen: Gebetsmühlenartig wird allerorten proklamiert, wir seien umfassend von Mathematik umgeben. Und für jede Person, die in letzter Zeit das Smartphone gezückt hat, Auto gefahren ist oder auch schlicht eine Ampel überquert hat, ist diese Aussage richtig. Was dabei oft nicht erwähnt wird: Diese alltägliche Mathematik ist meistens sehr schwierig. So schwer, dass die Schulmathematik sie bei Weitem noch nicht erfasst. So schwer, dass ihre Entwicklung zum Teil über 2000 Jahre gebraucht hat, obwohl man dafür nur Bleistift und Papier gebraucht hätte. Also, keine Illusionen: Mathematik ist kein Spaziergang; nicht mal ein Marathon; eher ein Iron Man 1. Und am Iron Man nimmt man nicht untrainiert teil. Man trainiert über Jahre hinweg. Das passiert in der Schule: Man beginnt mit dem Training und mit der Erwerbung von Kompetenzen wie Disziplin, Hartnäckigkeit und der steten Erweiterung der Frustrationstoleranz. Zusammengefasst ist die Mathematik in der Schule die Kreisliga und die Mathematik der Wettervorhersage die Champions League. Deswegen soll das Training zum einen Spaß machen und sich zum anderen sinnhaft anfühlen.
Hier also ein paar Beispiele, warum es gerechtfertigt ist, Mathematik auch „schön“ zu nennen:
1) Die Eulersche Identität
e^{i \pi}+1 = 0
Alternativ kann man das noch verrückter aufschreiben:
\cos(\pi) + i \sin(\pi) +1 = 0.
Die Formel ist ein Wörterbuch, das zwischen Winkelfunktionen und Exponentialfunktionen hin- und herübersetzen kann. Selbst wenn sie kryptisch wirkt: Sie verblüfft optisch allein dadurch, dass links etwas scheinbar kompliziertes steht, was auf der rechten Seite in einer harmonischen Null aufgeht.
2) Der Satz des Pythagoras
a^2 + b^2 = c^2
Diese Formel zur Berechnung von Seiten in einem rechtwinkligen Dreieck lernt man in der Schule bereits. Erst wenn man einmal Zahlen in die Gleichung einzusetzen versucht, merkt man, wie ungewöhnlich es ist, aus der Summe von Quadratzahlen eine neue Quadratzahl herzustellen. Das führt uns direkt zu…
3) Der Große Fermatsche Satz
a^n + b^n = c^n hat keine Lösung, wenn a, b, c und n größer als 2 sind.
Obwohl auch Mathematiklaien dieser Behauptung aus dem 17. Jahrhundert intuitiv zustimmen können, wurde der strenge Beweis erst 1994 erbracht. Der Beweis muss einen Umweg über elliptische Kurven gehen und bedient sich eines wunderschönen Tricks der Mathematik: Dem Widerspruchsbeweis. Dabei tut man zunächst so, als ob die Behauptung nicht stimme. Nach langer Rechnerei gelangt man mit dieser falschen Annahme in die Sackgasse eines Widerspruchs.
- Christian Spannagel, Professor für Mathematik und Mathematikdidaktik an der Pädagogischen Hochschule Heidelberg, erklärt den Großen Fermatschen Satz: https://doi.org/10.5446/19891 & https://doi.org/10.5446/19890.
4) Die harmonische Reihe
1 + \frac{1}{2} + \frac{1}{3} + \frac{1}{4} + \frac{1}{5} + \ldots = \infty
oder in schlau:
\sum \limits_{i \in \mathbb{N}} \frac{1}{i} = \infty
in sehr schlau:
\zeta(i) = \sum \limits_{i \in \mathbb{N}} \frac{1}{i^1} = \infty
Es dauert ein bisschen, ehe man dieser Formel über den Weg traut, denn die immer kleiner werdenden Zahlen, scheinen keinen nennenswerten Beitrag zur Summe zu liefern.
- Jörn Loviscach, Professor für Ingenieurmathematik und technische Informatik an der Fachhochschule Bielefeld und YouTube-Star für Mathegeplagte, erklärt die Divergenz der harmonischen Reihe mit Integral: https://doi.org/10.5446/10331.
5) Das Gesetz der Primzahlzwillinge
Zwei Zahlen heißen Primzahlzwillinge, wenn eine Zahl n und die Zahl n + 2 beide Primzahlen sind. Unbewiesene Vermutung: Diese Kombination kommt unendlich oft vor.
Primzahlen sind ein beliebter Spielplatz in der Mathematik. Als Grundbausteine der Zahlenwelt sind sie faszinierende Exoten. Gerade bei sehr großen Zahlen fällt es schwer zu glauben, dass zwei aufeinanderfolgende ungerade Zahlen wirklich Primzahlen sein können. Sie werden in der Tat dann auch immer seltener. Aber wie weit wir auch gehen, es scheint sich immer wieder ein neues Zwillingspaar zu finden. Das größte derzeit bekannte Paar wurde 2016 entdeckt und ist so groß, dass allein die Darstellung der Zahlen jeweils 388.342 Ziffern benötigt.
- Christian Spannagel philosophiert über die Struktur der Menge der Primzahlen und erläutert Primzahlzwillinge: https://doi.org/10.5446/19865.
6) Fraktale
Es gibt auch schöne Mathematik zum Anschauen, manchmal sogar zum Anfassen. Besonders ästhetisch sind Fraktale (hier schön erklärt und mit hübschen Beispielen). Dabei handelt es sich um ein geometrisches Muster als Baustein, das sich in verschiedenen Skalierungen zu einem Gebilde zusammensetzt (so zum Beispiel ein Würfel aus Würfeln in der folgenden Abbildung).

Das Wort beschreibt (wie das Wort Fraktur) einen Bruch und beschreibt die gebrochene Dimension. Der Mathematiker Benoît Mandelbrot beschäftigte sich mit der Frage, wie lang die Küste Großbritanniens sei und stellte fest, dass die Antwort davon abhängt, wie nah er an die Küste heranzoomt, da sie immer neue kleine Windungen und Ausbuchtungen hat bis hin zum kleinsten Sandkorn, welches wiederum mit einer rauen Oberfläche eine unendliche Länge besitzt. Mandelbrot definierte eine rekursive Folge, die ein wunderschönes Fraktal erschafft. Fraktale begegnen uns an den banalsten Orten: Farnblätter entfalten sich fraktal, Blumenkohl ist fraktal aufgebaut und sogar in der Musik gibt es selbstähnliche Muster.

- Der Vater der Fraktale, Benoît Mandelbrot, spricht auf dem Weltmathematikerkongress über „Rauheit“ in der Mathematik, den Naturwissenschaften und der Kunst und regt an, auch für Schönheit im Groben und Wilden offen zu sein: https://doi.org/10.5446/15965.
- Die Autobiographie Mandelbrots ist nicht minder erstaunlich und ungewöhnlich als seine Entdeckung der Fraktale: https://tib.eu/bmandelbrot.
7) Die Keplersche Vermutung
Die Keplersche Vermutung ist ein Beispiel dafür, dass Obsthändler Jahrhunderte lang schlauer waren als alle Mathematikerinnen und Mathematiker der Welt. Vielleicht ist das sogar immer noch so, denn bisher wurde sie nur von einem Computer bewiesen. Die Keplersche Vermutung fragt danach, wie man Äpfel möglichst platzsparend stapelt. Mathematisch ausgedrückt sucht sie nach der optimalen oder dichtesten Kugelpackung (vgl. Abbildung).
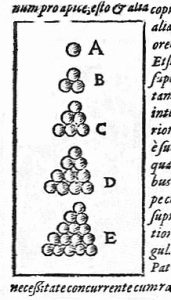
- Zur 400jährigen Geschichte der Keplerschen Vermutung, der sich sogar Johann Carl Friedrich Gauß geschlagen geben musste, und ihrem umstrittenen Computerbeweis: https://tib.eu/keplervermutungebook oder https://tib.eu/keplervermutungprint.
Computerbeweise gehören zu den großen Glaubensfragen in der Mathematik; manche Mathematikerinnen und Mathematiker lehnen sie kategorisch ab. Der erste berühmte Computerbeweis war die Lösung des…
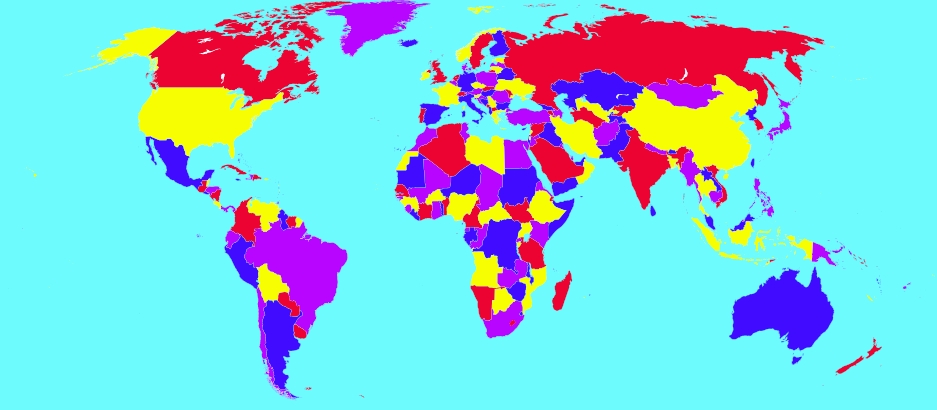
8) Vier-Farben-Problem
Die Behauptung klingt simpel und schwer zu glauben: Die Länder einer jeden erdenklichen Landkarte lassen sich mit nur vier Farben anmalen, ohne dass zwei aneinandergrenzende Länder die gleiche Farbe besitzen. Die Vermutung musste fast 150 Jahre alt werden, ehe sie bewiesen wurde. Der Beweis ähnelt einem Trial-and-Error-Ansatz: Man kategorisiert auftretende Kombinationen, und löst jede einzelne Kategorie. Beim Vier-Farben-Satz waren es stolze 633 Kategorien, die von einem Computer nachgeprüft wurden. Zugegeben: hier fehlt die Eleganz der Mathematik, und sie kommt eher etwas ungehobelt daher. Deswegen ist die Mathematik noch nicht fertig mit diesem Problem. Wenn wir Mathematikerinnen und Mathematiker einen Beweis hässlich finden, arbeiten wir so lange weiter daran, bis wir eine ästhetische Lösung gefunden haben.
9) Gödelscher Unvollständigkeitssatz
Der philosophischste Satz in der Mathematik besagt, dass jedes formale System (z. B. das System der natürlichen Zahlen und der vier Grundrechenarten, der Arithmetik) Grenzen hat. Es gibt also nicht nur Aussagen, die wahr oder falsch sind, sondern darüber hinaus unbeweisbare Aussagen. Dieser Satz ist eine Lektion in Demut für alle Rechthaber, die ihr Heil in der Mathematik suchen. Ihnen entwindet sie sich in diesem eleganten Satz und lässt uns mit den entscheidenden Fragen im Leben allein.
- Harald Sack, Informatikprofessor am Karlsruher Institut für Technologie, spricht im Rahmen einer Logikvorlesung über den Gödelschen Unvollständigkeitssatz: https://av.tib.eu/media/14265#t=04:01,10:27.
- „Eine geführte Reise durch Kurt Gödels historischen Beweis“ mit sozialer und wirtschaftlicher Einbettung, O-Tönen damaliger Kollegen und einer sensiblen Einführung in die mathematische Logik: https://tib.eu/goedelebook.
- Rebecca Goldsteins Gödel-Biographie ist nicht nur einfühlsam erzählt, sondern illustriert auch, dass sich die Persönlichkeit des Mathematikers in seinem Schaffen widerspiegelt: https://tib.eu/goldsteingoedel.
- Die Naturwissenschaftler Manfred Eigen, Hans Frauenfelder, Hermann Haken und Peter Schuster diskutierten schon 1985 als illustres Quartett über philosophische Aspekte und die Ästhetik der Mathematik: https://av.tib.eu/media/11192#t=26:19,28:20.
10) Zu guter Letzt….
… bildet die Mathematik auch das Studileben wunderschön ab:
\textrm{Studen}(t) = \int \limits_{\textrm{fr\"uh}}^{\textrm{sp\"at}} \mu de .
Und wofür braucht man das jetzt?
Die obige, subjektive Top Ten hat hier nur den Zweck des Genusses. Wenn sie Neugier geweckt oder ein Stirnrunzeln gezaubert hat, war dieser Artikel nicht umsonst. Trotzdem sind sie nicht reiner Selbstzweck. Mal laufen die Entwicklungen den Bedürfnissen anderer Fächer hinterher, mal greifen andere Fächer dankbar kontemplative Gedankenexperimente auf.
Hoffentlich konnte ich Sie ein bisschen mit der Mathematik versöhnen. Selbst wenn Sie mir nun nicht glauben, dass sie keine Kunst sei, die Vermittlung von Mathematik ist es. Einfühlungsvermögen, Fantasie und Spieltrieb sind Voraussetzungen dafür, Mathematik selbst genießen. Und diesen Genuss weiterzuvererben.
Quellen und noch mehr schöne Mathematik (auch zum Verschenken geeignet):
- Die offene Interaktionsplattform IMAGINARY zeigt in ihrer Galerie https://imaginary.org/galleries einige der schönsten mathematischen Gebilde, die bisher mit der Software erstellt wurden. Gleichzeitig lädt sie zum Mitmachen ein.
- Die schönsten Visualisierungen der Mathematik stellt das Buch „Bilder der Mathematik“ vor. Die Phänomene werden zwar erläutert, aber auch ohne Erklärungen lässt sich in den Bilder schwelgen: https://tib.eu/bilderdermathematik.
- Da es keinen richtigen und keinen falschen Weg zum Verständnis von Mathematik gibt, hier noch ein Beispiel für einen recht jungen und erfolgreichen Ansatz, nämlich Comics, Graphic Novels und Mangas: https://tib.eu/statistikmanga.
- In Deutschland hat sich vermutlich Albrecht Beutelspacher um die öffentliche Verbreitung von Mathematik auf unterhaltsame Weise verdient gemacht wie kein Zweiter. Unter anderem veröffentlichte er „Wie man in eine Seifenblase schlüpft“ mit 100 spannenden Matheexperimenten und „In Mathe war ich immer schlecht…“, ein Blick mit Augenzwinkern in das Innenleben der Mathematik und ihrer Knechte: https://tib.eu/seifenblase und https://tib.eu/inmathewarichimmerschlecht.
- Stets unterhaltsam ist auch die verquere Wahrnehmung von Wahrscheinlichkeiten, welches in den Büchern „Das Ziegenproblem: Denken in Wahrscheinlichkeiten“ und „Der Hund, der Eier legt“ aufgegriffen wird: https://tib.eu/ziegenproblem und https://tib.eu/hunddereierlegt.
Mila Runnwerth mit freundlicher Unterstützung von Bastian Drees, Christian Hauschke, Jenni Rügge und Stefan Schmeja

